Humankind has been inspired by Nature in several of its cutting-edge technologies. From airplanes, and submarines to sonar communications, evident plagiarism (ahem.. inspiration!) of "Nature" is seen. Few measure the advancement of technology on how well we mimic the complexity of the natural order we all have been dwelling in. It is logical to think that if the boundaries of our scientific evolution have to push beyond, we imitate the most complex computing system nature has ever provided. Our brains are those complex biological computing machines representing "Natural Intelligence.". As this mimicry leads to an artificial product created by humankind, it is called "Artificial Intelligence."
Simplifying a complex architecture to learn basics:
Let's not think about super complicated categorization or classification of branches of Artificial Intelligence or Machine Learning. We came here to talk about Neural Networks & we shall diligently do that. Just think of Neural Networks as an utter simplified model of the brain.
A general approach ( from a handful of folks I talk to) to learning Neural Networks is not to be self-confused by a complex mixture of mathematical terms, models & technical articles, or publications all at once, especially if you are a beginner with the below average mathematical background. Rather, try to visualize the brain as a huge network of fundamental nodes called Neurons that are interconnected, as seen from the above simplification of the brain to a bunch of neurons at the end. Using this simple notion of interconnected neurons, we shall weave in several concepts and simple math at a reasonable pace to establish an information processing mechanism in it. We shall use "Neuron" & "Node" terms interchangeably.
Overview of the mechanism:
Input data is converted into several sub-questions, each given to a separate node to answer. As each node receives a simple "True" or "False" question (not always that simple but play along for now!), a choice is made based on the learning it gained. This assignment of sub-questions to several nodes happens parallelly.
Next, we shall explore how distinguished learning is imparted to each of these nodes & then examine the notion of layers (groups of nodes). As a layer attempts to answer all your sub-questions, only a handful of them are solved while the rest remains unsolved. So we need to pass them to the next layer. This process continues until a reasonable decision has arrived at the output layer. This process is comparable to rainwater seeping into several layers of earth and reaching the water table.
 |
| The above explanation might have triggered this imagination of layers. This is partly true except that these layers are visualized from left to right, instead of top to bottom. |
Neurons & types:
A neuron accepts input information from its noodles-like structures called Dendrites on its head and outputs decisions through a long stem-like canal called the Axon. When a neuron likes to output info, it is said to be activated. It fires an electric impulse called "Action Potential" through Axon to its neighbors. Unless a neuron's input information is considerable level (threshold), it can't output any action potential. All inputs below this threshold fail to get neurons to activate and fire. This threshold is called the "Activation Threshold." An artificial neuron model called "Perceptron" is modeled after this behavior.
A Perceptron neuron can output either 0(False) or 1(True). So for a question like "Is this a hat ?", Perception can say either "Yes" or "No." If you chose any deceptively looking headcloth/bandana fashioned into a hat, your Perceptron outputs "Yes, it's a hat" if it is not trained enough (or) says "No, that ain't a hat!" if it had trained well to outsmart this deception. There isn't a benefit of doubt expressed through "Maybe" or "Perhaps" answers because neither "0" nor "1" can fit these words. "Activation Threshold" of your Perceptron can be programmed to output a "1" value by training it. Geez, this Perceptron can either be nothing..
Due to its primitive functionality, the Perceptron model cannot have a middle ground & it is not easy to train every possible picture of a hat in this universe through single/teamed human efforts. So a reasonable benefit of the doubt can fill those gaps. You can refer to publicly available datasets such as https://scale.com/open-datasets.
Think of a rating system from "1" to "10", with "1" being the lowest (or) NO and "10" being absolutely (or) YES. You now have the freedom to choose several points within this range to play middle ground for identifying a deceptively looking headcloth. This "1" to "10" rating allows you to guess close enough to the actual answer. A "Sigmoid" neuron do this "sort of" guess.
Its answer range has more intermediate values between and inclusive of "0" and "1," instead of just "0" & "1." For an input such as a deceptively looking hat, it can provide a confidence score of "0.866" instead of "1" to say "most likely!". However, there is a limit to this freedom as well. Why? There should be consistency in the output behavior of any model. Without any output behavioral pattern, it is impossible to control the behavior of your models and train them as you may be in constant fear, thinking how wild it can go with its guesswork without knowing what it is about to say next. A Sigmoid neuron output always follows a sinusoidal function on a 2D graph. Can you guess the output graph of Perceptron? An all-or-nothing kind of output always follows a step function.
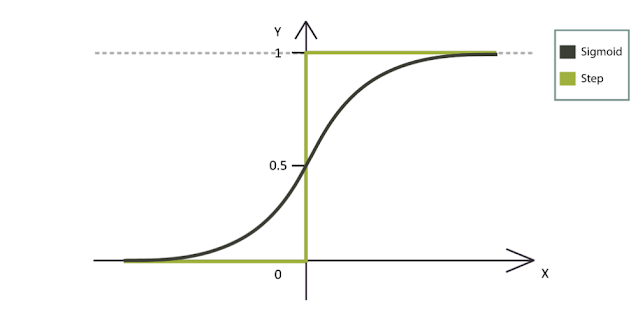 |
| https://ai-master.gitbooks.io/logistic-regression/content/weights.html |
Does x mark the spot?
Let's try understanding the graph with more insight. The X-axis (horizontal line) represents the data input our neural network has been receiving. Y axis (vertical line) represents the result that our neural output has been saying. The above graph says that until X values "0," y values remain "0.". In other words, until there is a positive or "0" valued input to the neural network, its result is always "0." "0" and positive x-values are activation thresholds for this neuron (if it is a perceptron and its threshold is tuned to "0").
A sinusoidal function shows positive Y values even for a few negative values of x. So it is a bit more forgiving than Perceptron. The negative value of x from where the graph starts rising to positive y values is the activation threshold for your sigmoid modeled neural network!
Getting serious, but not that serious...
I introduced you to two neuron models. Please don't hurry yet to think of what those "x" values are in the real world. They are not the pictures to be identified. "x" values here represent intermediate/middle stage processed information derived from a piece of the complete picture that a given neuron has. We shall further explore other stages and then discuss them comprehensively at the end.
The output shape from the neuron determines its type. The output from a Perceptron neuron looks like a step function on a 2D graph while a Sigmoid neuron outputs a sine or an "S" shaped function. There are mathematical expressions for all these graphs. These output functions are "Activation Functions." We shall follow the "σ(z)" notation for the Activation function.
You can glimpse (Don't seriously read its literature yet! You are not ready) https://vitalflux.com/different-types-activation-functions-neural-networks/ to get the feel of the wide variety of Activation Functions available in the world of the neural network.
We follow a method to train a neuron to process input information. And that method is from Master Oogway:
"Through experience, you shall learn to give relative importance(s) to several facts you see of a situation before reaching a final conclusion"
Think about it. Oogway's wisdom is good advice for all scenarios in our lives (You are welcome for Philosophy 101). Let's think from a robot's eye perspective. Through its camera lens, it is trying to understand whether a birthday party is happening in the cafeteria corner of the office.
There are several inputs ( for a total of "100" points, "100" is 100% surety) to be considered here:
a) Is there a moderate to a large group of people? Any event needs a group of people. ( "10" points )
b) A cake on a table. It could be a birthday cake or a successful launch celebration cake. ("30" points)
c) A center person near the cake who could be celebrating a birthday ("20" points)
d) Decorations or decorative writings with inclusive words "Happy Birthday!" ("40" points)
Do you see where I am going with this? I gave the highest points to decorations as they are the most important clues for our robot to deduce what's going on. In comparison to decorations, other hints come next in preference as these are present for any other celebration. If decorative writings are missing & other clues are present, those clues are accepted. That gives a 60% chance that it can be a birthday. If our robot is not programmed to engage in social conversations, it should conclude with a deduction of 60% probability of a birthday without speaking to people. So an error margin of 40% has crept here due to a lack of details. Algorithms such as these play on the level of probabilities all the time.
In the neural world, we call this relative importance "Weights." Treat the above checklist as inputs for our robot. A checklist of inputs with weights is called "Weighted Inputs.". For example, an input d (called "Decorations") has a maximum weight of "40" points! A weighted input d carries the value "d" multiplied by "40." Relatively, it has more weight when compared to others as this is the most valuable input of all inputs our robot can get to conclude whether it's a birthday party or not. If all inputs are present, we get a score of 100 points to confirm a birthday party. This score of "100" points is the "Weighted sum" of all inputs. The Weighted Sum is the addition of all weighted inputs.
The calculation "ax10+bx30+cx20+dx40= Weighted Sum" provides a number to conclude the "Whole" situation by giving relative importance to "several clues" in the situation. Though these inputs are presented here in statements, their presence can be represented by either 0 (absent) or 1 (present) by logic. So "1x10+1x30+1x20+1x40 = 100" says all inputs present. No decorations? "1x10+1x30+1x20=60" is the adjusted weighted sum.
So the final score of "100" or "60" represents the input here but wait! We as humans know that "60" out of "100" is a decent probability. How should we tell the robot that this is a decent probability of being a birthday celebration? Our old friend "Activation function" comes to the rescue. So by equation,
Activation function (Weighted Sum) = Result
This formula says that a weighted sum must feed the Activation function to give a result (Yay or nay) as the final result. This concludes the two stages of processing within any neuron. Few neuron models might employ a scheme other than the weighted sum scheme. Concept-wise, they are all attempting to do the same, providing a single score as an input to the activation function that can represent the whole situation ( multiple inputs ). This "Weighted Sum" scheme or another scheme to arrive at a representative score is called "Transfer Function". A weighted sum is represented as Z.
Below are important formulae:
Stage-1: Transfer function Z = ΣXn.Wn
Stage-2: Activation function σ(z) = σ(ΣXn.Wn)
where Xn is the nth input, ranging from 1 to N. N is the total number of inputs & Wn is the weight of Xn input. If N=1, then X1 is the first input and W1 is X1's weight. "." means dot product or multiplication of X & W. Ideally, this dot product should be used for vectors in a 2D or 3D space. I chose the dot product symbol in place of "x" to avoid confusion as there is already an "X" in the above formula. "Σ" is the summation symbol. It denotes the addition of parameter(s) that follow it in the formula.
Take an input X1 and multiple it by its weight W1 and keep it aside. Get another input X2 & multiple by its weight W2 to get "X2.W2" and add to the previous product "X1.W1". Repeat this procedure for all inputs and corresponding weights. This would give you "X1.W1 + X2.W2+......+Xn.Wn" Now feed this as input to your activation function.
Above is an x-ray of Perceptron neuron internals. A Perceptron neuron has a Threshold output function. Meaning, that any weighted sum which is less than "1" when fed to Perceptron will give a "0" result. Any Weighted sum value greater than or equal to "1", when given to it, will yield a "1" value. "1" or ">1" is the Threshold value for the Perceptron neuron to fire the output 1. You might be wondering why a constant "1" input is fed with weight W0. This is sometimes referred to as Bias or Bias Shift(b). So weighted sum of that linkage is "1".W0 = W0 = b. This is a trainable weight to shift your output graph in any direction you need in a 2D or 3D coordinate system (X, Y & Z axes). Useful to identify several similar cases in one neural network while training it. Don't think too much about bias now as it is reserved for intermediate learners. If you are curious about a 3D space graph with a bias, refer to the below animation or skip over it.
 |
| https://stackoverflow.com/questions/2480650/what-is-the-role-of-the-bias-in-neural-networks |
For the Sigmoid neuron, we have the below standard formula:
where e is a mathematical constant approximately equal to 2.71828. Just substitute your ΣX.W in above "x" and output is derived. The value of the total weighted sum (whether a positive or negative value, depending on the scale of x-axis you chose) for which the sinusoidal wave starts emitting positive values (or) starts to rise can be thought of as the threshold value for the sigmoid neuron. Irrespective of your weighted sum value, the output always follows a sinusoidal wave.
Layers:
So far, we have studied two legacy neuron models. Modern neural networks have neurons with far more sophistication than these models. A Deep Neural Network has several neurons (billions of them!). These neurons are arranged into several layers depending on either their role or the type of activation function they use. For example, the above diagram shows blue-colored neurons that accept input data. These blue neurons constitute the input layer. Neurons of the input layer convert input information to an understandable form and pass it to a hidden layer. Any layer between the input layer & output layer is called the "Hidden Layer." They perform several computations. There can be more than one hidden layer ( Deep Neural Networks: DNN ). All connections going from a neuron of the input layer to a neuron of an adjacent hidden layer carry corresponding weight values. Similar weighted connections happen among all hidden layers. The last hidden layer passes its results to the output layer. We have an output layer (green bubbles) to provide final results in a compatible format to an interface ( a software, a display, or other hardware ).
Hidden layers are created based on the type of neurons in them. Let's say you want a group of neurons acting as Perceptrons & another group as Sigmoids. A Perceptron hidden layer comprising of perceptron nodes followed by a Sigmoid hidden layer comprising of sigmoid nodes can be your total hidden layers between input and output layers. The depth of DNN is equal to its total number of hidden layers.
Let's say your neural network needs to identify a type of hat. Your Neural network divides the image of a hat into four quadrants (pieces) and feeds each piece to individual neurons in its input layer. Input layer neurons convert those pieces to a form understandable by neurons on the hidden layer. The topmost neuron in the first hidden layer may have the role of identifying whether there is a curved edge in the piece it received. Another neuron of the same layer identifies another part of the hat through the input it receives. This divide & conquer process of the actual problem is called "Decomposition." Finally, the result from the last hidden layer passes to the output layer.
Training:
 |
| Dr. Hermann Gottlieb from Pacific Rim 2013: Numbers don’t lie. Politics, poetry, promises… these are lies. Numbers are as close as we get to the handwriting of God |
Dr. Hermann warned Stacker Pentecost of the double event ( 2 Kaiju monsters emerging from tectonic plate fissure portal on ocean bed ) to occur in 4 days while being competed by Dr. Newton Geiszler at Shatterdome. He relied on statistical data & in a way, created a prediction model similar to a neural network model through meticulous calculations. With our neural network schema assembled, we can start training it with lots of data to be reliable similar to Hermann's model that went on to save humanity. Huge props to Newton too!
We begin by assigning random & yet reasonable scaled numerical values to our weights & feed already available data with results to our neurons. They process the info & output results depending on their activation function. You can compare the model's output with the actual results in data & get the difference, the error margin. Later, we adjust the weights of our inputs to provide us with a different weighted sum & a different output is seen from our activation function but with a much lesser error margin than before. This process is continued until the error margin is either negligible or saturates. We can then conclude that our training is complete & our model is ready to face the world.
The training sequence of a neural network is called "epochs" or "iterations." Depending on other nuts & bolts you chose for your model, there may be a few parameters that shouldn't change during training & have to be fixed before epochs begin. They are called "Hyperparameters" & the process of setting them is called "Hyperparameter tuning.". Your neural network adapts with training. A neural network can perform three types of learning. With supervised learning, your neural network model is given several "Hat" pictures with an indication or a label that they are all hats. A network is supposed to adapt its weights eventually to recognize a hat from an unlabeled picture post-training. Unsupervised learning removes the labels from all "Hat" pictures and lets the network model recognize a pattern to identify a hat post-training. Semi-supervised learning is the combination of both styles.
That's a lot. I get it. But hey, you are now a graduate of Neural networks basics. In my eye, you are no longer a beginner. The next article shall be at an intermediate level. Maybe watch an episode of Friends on HBO Max or Youtube Movies and come back later for the upcoming article. But if you think you are done at this point, well, it's been nice having you here. Take care ...









.png)
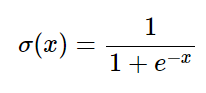





.png)

No comments:
Post a Comment
Please refrain from abusive text.
Note: Only a member of this blog may post a comment.